

In a certain college 60% of all students are female, and 10% of all students are computer science majors. The following problem illustrates this point. Whenever communicating about a percentage, it is important to specify what it is relative to (i.e., what is the total that corresponds to 100%). A term such as 100 / 100% would also be incorrect, since it would be read as 1 percent, even if the intent was to say 100%. It is not correct to divide by 100 and use the percent sign at the same time it would literally imply division by 10,000. To calculate a percentage of a percentage, convert both percentages to fractions of 100, or to decimals, and multiply them. The percent value can also be found by multiplying first instead of later, so in this example, the 50 would be multiplied by 100 to give 5,000, and this result would be divided by 1250 to give 4%. For example, to find 50 apples as a percentage of 1250 apples, one first computes the ratio 50 / 1250 = 0.04, and then multiplies by 100 to obtain 4%. The percent value is computed by multiplying the numeric value of the ratio by 100. The "cento" was contracted to two circles separated by a horizontal line, from which the modern "%" symbol is derived. The "per" was often abbreviated as "p."-eventually disappeared entirely.
The sign for "percent" evolved by gradual contraction of the Italian term per cento, meaning "for a hundred". The term "percent" is derived from the Latin per centum, meaning "hundred" or "by the hundred". Main article: Percent sign A percent sign By the 17th century, it was standard to quote interest rates in hundredths. Many of these texts applied these methods to profit and loss, interest rates, and the Rule of Three. Computation with these fractions was equivalent to computing percentages.Īs denominations of money grew in the Middle Ages, computations with a denominator of 100 became increasingly standard, such that from the late 15th century to the early 16th century, it became common for arithmetic texts to include such computations. For example, Augustus levied a tax of 1 / 100 on goods sold at auction known as centesima rerum venalium.
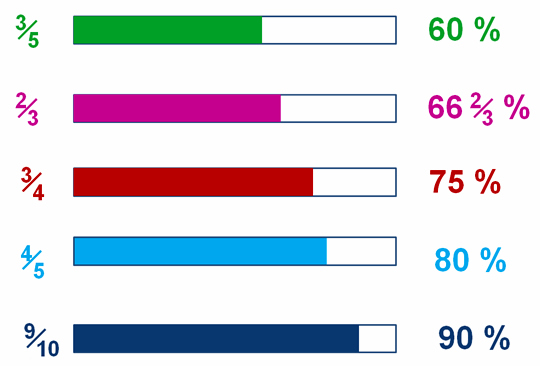
In Ancient Rome, long before the existence of the decimal system, computations were often made in fractions in the multiples of 1 / 100. For example, it is common to refer to 111% or −35%, especially for percent changes and comparisons. While many percentage values are between 0 and 100, there is no mathematical restriction and percentages may take on other values. Expressed as a percentage, this is a 6% increase. If there are 500 students, then 250 of them are male.Īn increase of $0.15 on a price of $2.50 is an increase by a fraction of 0.15 / 2.50 = 0.06. If 50% of the total number of students in the class are male, that means that 50 out of every 100 students are male. (Similarly, one can also express a number as a fraction of 1,000, using the term " per mille" or the symbol " ‰".) Percentages are often used to express a proportionate part of a total. Examplesįor example, 45% (read as "forty-five per cent") is equal to the fraction 45 / 100, the ratio 45:55 (or 45:100 when comparing to the total rather than the other portion), or 0.45. A percentage is a dimensionless number (pure number), primarily used for expressing proportions, but percent is nonetheless a unit of measurement in its orthography and usage.
#FRACTIONS INTO PERCENTAGES CALCULATOR PC#
It is often denoted using the percent sign (%), although the abbreviations pct., pct, and sometimes pc are also used. In mathematics, a percentage (from Latin per centum 'by a hundred') is a number or ratio expressed as a fraction of 100. For the unit of currency, see cent (currency).Ī pie chart showing the percentage by web browser visiting Wikimedia sites (April 2009 to 2012)


 0 kommentar(er)
0 kommentar(er)
